Question

SOMEONE PLEASE ANSWER
the equation is 7x-3 over 9 > 8-2x

Answer 1

solving the inequality we get
`\mathbf{x\geq 3}`

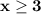
The graph is attached below.

Option C is correct option.

Explanation:

We need to solve the inequality
`(7x-3)/(9)\geq 8-2x`

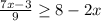
First we will solve the inequality to find value of x

Solving:

`(7x-3)/(9)\geq 8-2x`

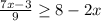
Step 1: Multiply both sides by 9

`9((7x-3)/(9))\geq 9(8-2x)\\7x-3\geq 72-18x`

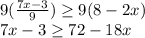
Step 2: Adding 3 on both sides

`7x-3+3\geq 72-18x+3\\7x\geq 75x-18x`

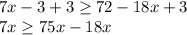
Step 3: Add 18x on both sides

`7x+18x\geq 75-+18x\\25x\geq 75`

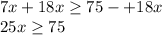
Step 4: Divide both sides by 25

`(25x)/(25)\geq (75)/(25)\\x\geq 3`

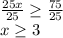
So, solving the inequality we get
`\mathbf{x\geq 3}`

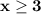
The graph is attached below.

Option C is correct option.