Question

PLEASE HELP!!!

what is the average rate of change of the equation: y=4x^2-10x+2, between f(3) and f(5)? ​

Answer 1

Average rate of change=22

Explanation:

We need to find the average rate of change of the equation:
`y=4x^2-10x+2`between f(3) and f(5).

The formula used to find average rate of change is:
`Average \ rate \ of \ change=(f(b)-f(a))/(b-a)`

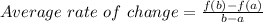
In the given question we have a=3 and b =5

Finding f(a) i.e f(3)

`f(3)=4(3)^2-10(3)+2\\f(3)=4(9)-30+2\\f(3)=36-30+2\\f(3)=8`

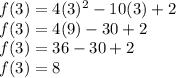
Finding f(b0 i.e f(5)

`f(5)=4(5)^2-10(5)+2\\f(5)=4(25)-50+2\\f(5)=100-50+2\\f(5)=52`

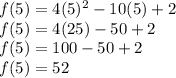
Putting values of f(3)=8 and f(5)=52 to find average rate of change

`Average \ rate \ of \ change=(f(b)-f(a))/(b-a)\\Average \ rate \ of \ change=(52-8)/(5-3)\\Average \ rate \ of \ change=(44)/(2)\\Average \ rate \ of \ change=22`

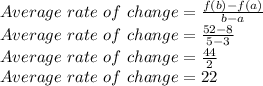
So, Average rate of change=22