Final answer:
The formula for solving s in terms of the surface area and radius of a cone is s = (S - 2πr)/(πr). For a given surface area of 220 square feet and radius of 7 feet, the slant height is approximately 9.3 feet.
Step-by-step explanation:
To solve the formula for s, we need to isolate s on one side of the equation. The formula is given by:
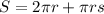
Step 1: Subtract 2πr from both sides of the equation to isolate the rs term:
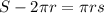
Step 2: Divide both sides of the equation by πr to solve for s:
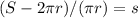
Therefore, the formula for s is s =
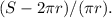
To find the slant height when the surface area is 220 square feet and the radius is 7 feet, substitute the given values into the formula:
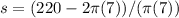
Calculate the value of s using a calculator to obtain a value of approximately 9.3 feet.