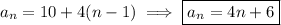Question

A1=10an=an-1+4 ??????? help pls

Answer 1

I assume you're asked to solve for
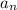`a_n`, or find an explicit formula for the n-th term in the sequence.

The sequence is recursively defined by

`\begin{cases} a_1 = 10 \\ a_n = a_(n-1) + 4 & \text{for } n \ge 1 \end{cases}`

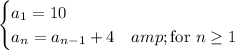
By this definition,

`a_(n-1) = a_(n-2) + 4`

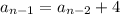
so that by substitution,

`a_n = (a_(n-2) + 4) + 4 = a_(n-2) + 2*4`

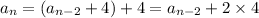
and we can repeat this process to find

`a_n = a_(n-3) + 3*4`

`a_n = a_(n-4) + 4*4`

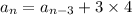
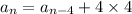
and so on, down to

`a_n = a_1 + (n-1)*4`

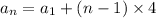
Then given the first term
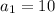`a_1=10`, we have

`a_n = 10 + 4(n-1) \implies \boxed{a_n = 4n + 6}`