Question

Sheer industries is considering a new computer-assisted program to train maintenance employees to do machine repairs. In order to fully evaluate the program, the director of manufacturing requested an estimate of the population mean time required for maintenance employees to complete the computer assisted training. Use 7.94 days as a planning value for the population standard deviation.

Answer 1

The question is missing parts. Here is the complete question.

Sheer Industries is considering a new computer-assisted program to train maintenance employees to do machine repairs. In order to fully evaluate the program, the director ofmanufacturing requested an estimateof the population mean time required for maintenance employees to complete the computer assisted training. Use 7.94 days as a planning value for the population standard deviation. (Round your answers up to the nearest whole number).

(a) Assuming 95% confidence, what sample size would be required to obtain a margin of error of 0.5 days?

(b) If precision statement was made with 90% confidence, what sample size would be required to obtain a margin of error of 3 days?

Answer: (a) n = 900

(b) n = 18

Explanation: Margin of Error represents the percentage of confidence your result will be different from the real population value.

It is calculated as

`E=z(\sigma)/(√(n))`

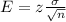
z is z-score related to the percentage of confidence

σ is population standard deviation

n is sample size

(a) Margin of error = 0.5

For a 95% confidence, z-score is 1.96.

Sample size will be:

`E=z(\sigma)/(√(n))`

`√(n)=(z\sigma)/(E)`

`√(n)=(1.96*7.64)/(0.5)`

`√(n) =30`

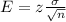
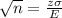
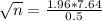
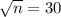
n = 900

For a 95% confidence, margin of error of 0.5 days, sample size required would be 900.

(b) Margin of error = 3

z-score for 90% confidence = 1.645

Solving for sample size:

`√(n)=(z\sigma)/(E)`

`√(n)=(1.645*7.64)/(3)`

`√(n)=4.2`

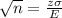
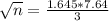
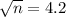
n = 18

It would be required, to obtain a margin of error of 3 days, a sample size of 18 maintenance employees.