Answer:
The trigonometric ratios associated with (-5, -4) are
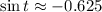 ,
,
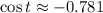 and
and
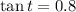 .
.
Explanation:
Let
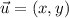 . From Trigonometry, we remember the following definitions for the trigonometric ratios, dimensionless:
. From Trigonometry, we remember the following definitions for the trigonometric ratios, dimensionless:
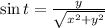 (1)
(1)
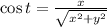 (2)
(2)
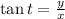 (3)
(3)
If we know that
 and
and
 , then the trigonometric ratios are, respectively:
, then the trigonometric ratios are, respectively:
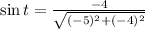
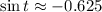
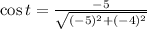
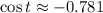
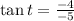
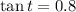
The trigonometric ratios associated with (-5, -4) are
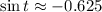 ,
,
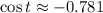 and
and
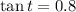 .
.