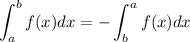Question

Calculus I integral problem

If

`\int\limits^4_0 {g(x)} \, dx = √(5)`
evaluate

`\int\limits^0_(-2) {xg(x^(2))√(7)} \, dx`

Answer 1

Answer:
`-(√(35))/(2)`

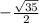
In terms of typing this in on a keyboard, you could say -sqrt(35)/2

===================================================

Work Shown:

We'll use u-substitution here

Let u = x^2, so du/dx = 2x which rearranges to du = 2x*dx and we can say xdx = du/2

Because we are changing from x^2 to u, this means we need to change the limits of integration

If x = -2, then u = x^2 = (-2)^2 = 4

If x = 0, then u = x^2 = 0^2 = 0

Despite 4 being larger than 0, we still place 4 at the bottom limit and we'll just swap them later.

This means we have the following steps

`\displaystyle \int_(-2)^(0)xg(x^2)√(7)dx\\\\\\\displaystyle √(7)\int_(-2)^(0)xg(x^2)dx\\\\\\\displaystyle √(7)\int_(-2)^(0)g(x^2)xdx\\\\\\\displaystyle √(7)\int_(4)^(0)g(u)(du)/(2)\\\\\\\displaystyle -√(7)\int_(0)^(4)g(u)(du)/(2)\\\\\\\displaystyle -√(7)*(1)/(2)\int_(0)^(4)g(u)du\\\\\\\displaystyle -(√(7))/(2)√(5)\\\\\\\displaystyle -(√(7)*√(5))/(2)\\\\\\\displaystyle -(√(7*5))/(2)\\\\\\\displaystyle -(√(35))/(2)\\\\\\`

Notice when I swapped the limits of integration (4 and 0 to 0 and 4) I placed a negative sign out front.

The rule is
`\displaystyle \int_(a)^(b)f(x)dx = -\int_(b)^(a)f(x)dx`