Answer: The numbers are 32 and 12
Explanation:
Let say those two positve integers are x and y.
x has to be 8 more than twice y , and that could be represent by the equation
x = 2y + 8
Their product is 384 meaning that x times y has to equal to 384 , and that can also be represented by the equation xy = 384
x = 2y + 8
xy = 384
Now using both equations, substitute the value for x into the second equation and solve for y.
(2y + 8)(y ) = 384
2y^2 + 8y = 384 Subtract 348 from both sides
-384 -384
2y^2 + 8y - 384 = 0 Factor the left sides by the GCF
2(y^2 + 4y - 192) = 0
x = -b ±

The variables a= 1 , b=4 and c is -192
x = -4 ±
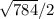
x = -4 + 14 or x = -4 - 14
x = 12 or x = -16
Since we are dealing with length the value of y has to be 12.
Now that we know that y is 12 input 12 into one of the equations and solve for x.
x = 2(12) + 8
x = 24 + 8
x = 32