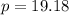Answer:
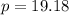
Explanation:
This question is illustrated using the attachment and will be solved using cosine formula
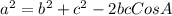
Let the strawberry side be s, the Green beans be b and the pumpkins be p.
The cosine formula in this case is:
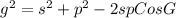
Where

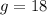
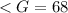
The equation becomes
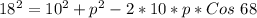
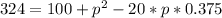
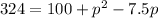
Collect Like Terms
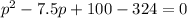
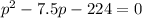
Using quadratic formula:
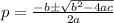
Where
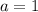


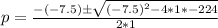
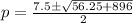
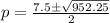
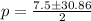
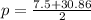 or
or

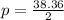 or
or

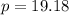 or
or

But length can not be negative.
So: