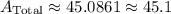Answer:
Explanation:
We can use the trigonometric formula for the area of a triangle:
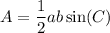
Where a and b are the side lengths, and C is the angle between the two side lengths.
As demonstrated by the line, ABCD is the sum of the areas of two triangles: a right triangle ABD and a scalene triangle CDB.
We will determine the area of each triangle individually and then sum their values.
Right Triangle ABD:
We can use the above area formula if we know the angle between two sides.
Looking at our triangle, we know that ∠ADB is 55 DB is 10.
So, if we can find AD, we can apply the formula.
Notice that AD is the adjacent side to ∠ADB. Also, DB is the hypotenuse.
Since this is a right triangle, we can utilize the trig ratios.
In this case, we will use cosine. Remember that cosine is the ratio of the adjacent side to the hypotenuse.
Therefore:

Solve for AD:
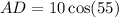
Now, we can use the formula. We have:
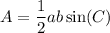
Substituting AD for a, 10 for b, and 55 for C, we get:
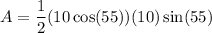
Simplify. Therefore, the area of the right triangle is:
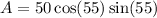
We will not evaluate this, as we do not want inaccuracies in our final answer.
Scalene Triangle CDB:
We will use the same tactic as above.
We see that if we can determine CD, we can use our area formula.
First, we can determine ∠C. Since the interior angles sum to 180 in a triangle, this means that:
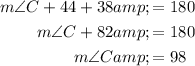
Notice that we know the angle opposite to CD.
And, ∠C is opposite to BD, which measures 10.
Therefore, we can use the Law of Sines to determine CD:
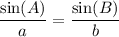
Where A and B are the angles opposite to its respective sides.
So, we can substitute 98 for A, 10 for a, 38 for B, and CD for b. Therefore:
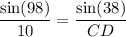
Solve for CD. Cross-multiply:
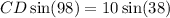
Divide both sides by sin(98). Hence:
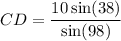
Therefore, we can now use our area formula:
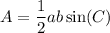
We will substitute 10 for a, CD for b, and 44 for C. Hence:
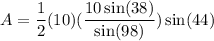
Simplify. So, the area of the scalene triangle is:
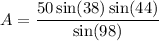
Therefore, our total area will be given by:
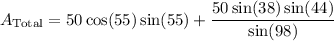
Approximate. Use a calculator. Thus: