Question

A satellite of mass 1.02 metric tons orbits Earth at a constant height. If the mass of Earth is 6 x 10^24 kg,its radius is 6,360 km,and the gravitational force between Earth and the satellite is 6.6 x 10^3 N, find the height of the satellite’s orbit rounded to the nearest kilometer. Take the universal gravitational constant, G = 6.67 x 10^-11 Nm^2/kg^2.

Answer 1

height = 1.5 x 10⁶ m = 1500 km

Step-by-step explanation:

We can use the formula of gravitational force from the Newton's Gravitational Law:

`F = (Gm_(1)m_(2))/(r^2)`

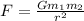
where,

F = Gravitational Force = 6.6 x 10³ N

G = Universal Gravitational Constant = 6.67 x 10⁻¹¹ N.m²/kg²

m₁ = mass of earth = 6 x 10²⁴ kg

m₂ = mass of satellite = (1.02 tons)(1000 kg/1 ton) = 1.02 x 10³ kg

r = distance between center of earth and satellite = ?

Therefore, using these values in the equation, we get:

`6.6\ x\ 10^3\ N = ((6.67\ x\ 10^(-11) N.m^2/kg^2)(6\ x\ 10^(24) kg)(1.02\ x\ 10^3\ kg))/(r^2)\\\\r^2 = ((6.67\ x\ 10^(-11) N.m^2/kg^2)(6\ x\ 10^(24) kg)(1.02\ x\ 10^3\ kg))/(6.6\ x\ 10^3\ N)\\\\`

`r = \sqrt{61.84\ x\ 10^(12)\ m^2 }`

`r = 7.86\ x\ 10^6 m`

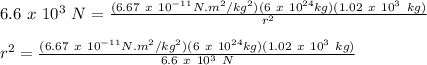
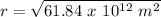
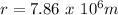
The distance between center of earth and the satellite is equal to the sum of height of satellite and radius of earth:

`r = height + radius\ of\ earth\\7.86\ x\ 10^6 m = height + 6.36\ x\ 10^6 m\\height = 7.86\ x\ 10^6 m - 6.36\ x\ 10^6 m`

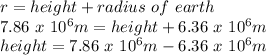
height = 1.5 x 10⁶ m = 1500 km