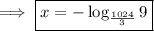1 Answer

Diane Kaplan · Answer 1 · 2021-12-21T02:31:31+0000

Take the logarithm of both sides. The base of the logarithm doesn't matter.

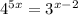
4^(5x) = 3^(x-2)

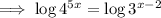
$\implies \log 4^(5x) = \log 3^(x-2)$

Drop the exponents:

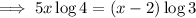
$\implies 5x \log 4 = (x-2) \log 3$

Expand the right side:

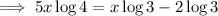
$\implies 5x \log 4 = x \log 3 - 2 \log 3$

Move the terms containing x to the left side and factor out x :

$\implies 5x \log 4 - x \log 3 = - 2 \log 3$

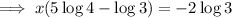
$\implies x (5 \log 4 - \log 3) = - 2 \log 3$

Solve for x by dividing boths ides by 5 log(4) - log(3) :

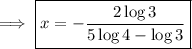
$\implies \boxed{x = -( 2 \log 3 )/( 5 \log 4 - \log 3 )}$

You can stop there, or continue simplifying the solution by using properties of logarithms:

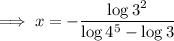
$\implies x = -( \log 3^2 )/( \log 4^5 - \log 3 )$

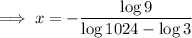
$\implies x = -( \log 9 )/( \log 1024 - \log 3 )$

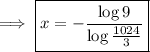
$\implies \boxed{x = -\frac{ \log 9 }{ \log \frac{1024}3 }}$

You can condense the solution further using the change-of-base identity,

$\implies \boxed{x = -\log_{\frac{1024}3}9}$

Please log in or register to add a comment.