Question

The function h(t) = -16t2 + 48t + 28 models the height (in feet) of a ball where t is the time (in seconds).

What is the maximum height that the ball reaches? Just write the numerical answer - do not include h = or any units in your
answer.

Answer 1

64

Explanation:

[using calculus] When the function h(t) reaches its maximum value, its first derivative will be equal to zero (the first derivative represents velocity of the ball, which is instantaneously zero). We have
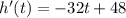`h'(t) = -32t + 48`, which equals zero when
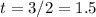`t = 3/2 = 1.5`. The ball therefore reaches its maximum height when t = 1.5. To find the maximum height, we need to find h(1.5), which is 64 feet.

[without calculus] This is a quadratic function, so its maximum value will occur at its vertex. The formula for the x-coordinate of the vertex is -b/2a, so the maximum value occurs when t = -48/(2*16), which is 1.5. The maximum height is h(1.5), which is 64 feet.