Question

How do you the equation of the line that passes through point (-3,2) and is parallel to the line formed by the equation y = 4x + 7?

need it urgently please , thanks​

Answer 1

y = 4x + 14

Explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

y = 4x + 7 ← is in slope- intercept form

with slope m = 4

• Parallel lines have equal slopes , then

y = 4x + c ← is the partial equation

to find c substitute (- 3, 2 ) into the partial equation

2 = - 12 + c ⇒ c = 2 + 12 = 14

y = 4x + 14 ← equation of parallel line

Answer 2

`\boldsymbol{y=4x+14}`

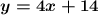
Explanation:

Hi student! Let me help you out on this question.

________

- - - - - - - - - - - - - - - - -

↪

PART 1

First of all we need to find, the slope of the line that is parallel to the line
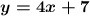`\boldsymbol{y=4x+7}`. Which is pretty easy, considering the fact that the slopes of parallel lines are the same.

The slope of the line
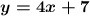`\boldsymbol{y=4x+7}` is
`\boldsymbol 4`.

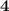Which means the slope of the line that is parallel to the one above is also 4.

- - - - - - - - - - - - - - - - -

↪

PART 2

Now we should find the equation of the line. We know that its slope is 4, so let's stick in 4 for the slope into the slope-intercept form equation:

(remember, m denotes the slope and b denotes the y intercept).

`\boldsymbol{y=mx+b}`

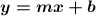
Stick in 4 for the slope.

`\boldsymbol{y=4x+b}`

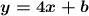
Note that we are also given a point that's on the line.

We can stick in its y-co-ordinate, 2. for y.

`\boldsymbol{2=4x+b}`

Now let's stick in -3 for x.

`\boldsymbol{2=4(-3)+b}`

Solve for b.

`\boldsymbol{2=-12+b}`

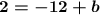
Add 12 to both sides.

`\boldsymbol{2+12=b}`

`\boldsymbol{14=b}`

↪

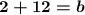
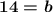
Now that we know the y-intercept, let's stick it into the slope-intercept form equation for b:

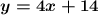`\boldsymbol{y=4x+14}`. Which is our final answer, the equation.

⇨Hope that this helped you out! Have a nice day ahead.⇦

Best Wishes!

`\star\bigstar\boldsymbol{Reach\:far.\:Aim\:high.\:Dream \ big.}}\bigstar\star`

◆◈-Greetings!-◆◈

- - - - - - - - - - - - - - - - - -

_____________