Answer:
a=6, b=2, c=6, d=2, e=6, f=6, g=1
Explanation:
You want the values of letters a–g that show the correct simplification of ...
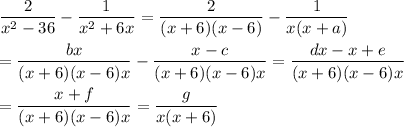
Solution
The difference of squares is factored as (a² -b²) = (a +b)(a -b), so the denominator of the first term can be factored. The common factor x can be factored out of the denominator of the second term. This gives ...
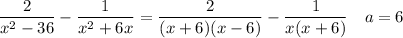
Multiplying the first term by x/x and the second term by (x-6)/(x-6) gives ...
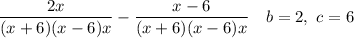
Writing the sum over the common denominator, we have ...
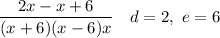
Collecting terms in the numerator gives ...
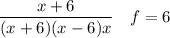
Finally, cancelling the common factor (x+6) from numerator and denominator, we have the simplified form ...

The values of the letters are ...
a=6, b=2, c=6, d=2, e=6, f=6, g=1