Question

HELP PLEASE ITS DUE TODAY!!!!!

Answer 1

Let's find.

`\\ \rm\Rrightarrow (-2x^3+x-5)(x^3-3x-4)`

`\\ \rm\Rrightarrow x^3(-2x^3+x-5)-3x(-2x^3+x-5)-4(-2x^3+x-5)`

`\\ \rm\Rrightarrow -2x^6+x^4-5x^3+6x^4-3x^2+15x+8x^3-4x+20`

`\\ \rm\Rrightarrow -2x^6+7x^4+3x^3-3x^2+11x+20`

#b

Yes

It's because multiplication law states that ab=ba

Answer 2

• -2x⁶ +7x⁴ +3x³ -3x² +11x +20
• equal both ways: commutative property of multiplication

Explanation:

The product of polynomials is found by multiplying each term of one by each term of the other and collecting terms. It is repeated application of the distributive property.

__

first application of distributive property

`(-2x^3+x-5)(x^3-3x-4)=-2x^3(x^3-3x-4)+x(x^3-3x-4)-5(x^3-3x-4)`

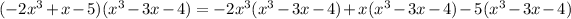
next application of distributive property

`=(-2x^6+6x^4+8x^3)+(x^4-3x^2-4x)+(-5x^3+15x+20)`

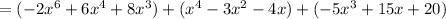
collecting terms

`=-2x^6 +(6+1)x^4 +(8-5)x^3-3x^2+(-4+15)x+20\\\\=\boxed{-2x^6+7x^4+3x^3-3x^2+11x+20}`

__

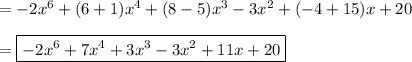
order swapped

Each term of one polynomial is multiplied by every term of the other. This will be the case regardless of which one is written first in the product. Multiplication of numbers and variables has commutative and associative properties, so the order does not matter. The products are equal.