Answer:
- -2x⁶ +7x⁴ +3x³ -3x² +11x +20
- equal both ways: commutative property of multiplication
Explanation:
The product of polynomials is found by multiplying each term of one by each term of the other and collecting terms. It is repeated application of the distributive property.
__
first application of distributive property
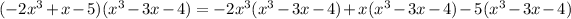
next application of distributive property
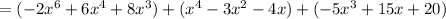
collecting terms
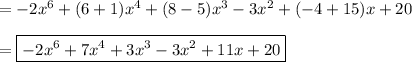
__
order swapped
Each term of one polynomial is multiplied by every term of the other. This will be the case regardless of which one is written first in the product. Multiplication of numbers and variables has commutative and associative properties, so the order does not matter. The products are equal.