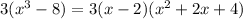Answer:
11.
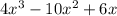
Take out 2x ( greatest common factor )

Factor
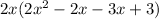
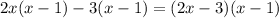
Don't forget about the 2x we took out earlier
Solution to 11:
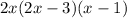
12.
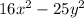
This is the difference of squares, so let's use the formula...
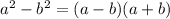
if,
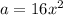 and
and
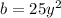
then, the Solution to 12 is:
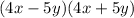
13.
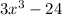
First of all, you must find the greatest common factor because there isn't anything else you can do.
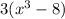
Now you can see the difference of cubes...
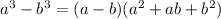
so, the Solution to 13 is: