Answer:
Volume of Cylinder = 300cm^3, Volume of 1 Cone = 100cm^3
Explanation:
Let r be the radius
Let h be the Height
Given r = h, we will take h as r.
Volume of cylinder
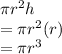
Volume of 2 cones
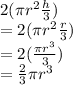
Given Total Volume = 500cm^3 = Volume of cylinder + Volume of 2 cones
![\pi r^(3) + (2)/(3)\pi r^(3) = 500 \\(5)/(3) \pi r^(3) = 500\\\pi r^(3) = 500*(3)/(5) \\\pi r^(3) = 300\\r^(3) = (300)/(\pi ) \\r=\sqrt[3]{(300)/(\pi ) } cm \\](https://img.qammunity.org/2023/formulas/mathematics/high-school/yl1e5wvnywj64mc36toaajjycfv39datl8.png)
Now we got r and r=h,
Volume of Cylinder
![\pi (\sqrt[3]{(300)/(\pi ) } )^(3)\\=\pi ((300)/(\pi ) )\\= 300cm^(3)](https://img.qammunity.org/2023/formulas/mathematics/high-school/lwly4is9dn6pfkrh3rr8q5i4sm5veqvvrw.png)
Volume of 1 cone = (Total Volume - Volume of Cylinder) / 2
= (500-300)/2
= 200/2
= 100cm^3