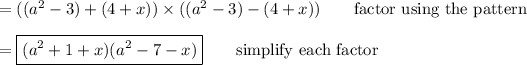Question

Factorize a⁴-6a²-7-8x-x²​

Answer 1

Answer:a⁴-7-x²-6a²-8x

Answer 2

(a² +x +1)(a² -x -7)

Explanation:

This expression can be factored by making use of the pattern for factoring the difference of squares. That pattern is ...

p² -q² = (p +q)(p -q)

__

rearrange to difference of squares

We can split the term -7 into the sum +9-16 so that parts of the expression can be written as squares.

`a^4 -6a^2-7-8x-x^2\\\\=(a^4-6a^2+9)-(16+8x+x^2)\qquad\text{use -7=9-16, group terms}\\\\=(a^2-3)^2-(4+x)^2\qquad\text{write as squares}`

factor using the pattern

`=((a^2-3)+(4+x))*((a^2-3)-(4+x))\qquad\text{factor using the pattern}\\\\=\boxed{(a^2+1+x)(a^2-7-x)}\qquad\text{simplify each factor}`