Question

How high does a rocket have to go above the earth's surface to be subject to a gravitational field from the earth that is 50.0 percent of its value at the earth's surface?

A) 2.650 km
B) 3,190 km
C) 9.020 km
D) 12.700 km​

Answer 1

A) 2.650 km

Step-by-step explanation:

The relationship between acceleration of gravity and gravitational constant is:

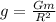`g = (Gm)/(R^2)` ---- (1)

Where

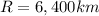`R = 6,400 km` -- Radius of the earth.

From the question, we understand that the gravitational field of the rocket is 50% of its original value.

This means that:

`g_(rocket) = 50\% * g`

`g_(rocket) = 0.50 * g`

`g_(rocket) = 0.5g`

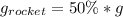
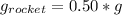
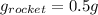
For the rocket, we have:

`g_(rocket) = (Gm)/(r^2)`

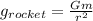
Where r represent the distance between the rocket and the center of the earth.

Substitute 0.5g for g rocket

`0.5g = (Gm)/(r^2)` --- (2)

Divide (1) by (2)

`(g)/(0.5g) = (Gm)/(R^2)/(Gm)/(r^2)`

`(g)/(0.5g) = (Gm)/(R^2)*(r^2)/(Gm)`

`(1)/(0.5) = (1)/(R^2)*(r^2)/(1)`

`2 = (r^2)/(R^2)`

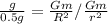
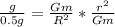
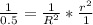
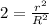
Take square root of both sides

`\sqrt 2 = (r)/(R)`

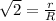
Make r the subject

`r = R * \sqrt 2`

Substitute
`R = 6,400 km`

`r = 6400km * \sqrt 2`

`r = 6400km * 1.414`

`r = 9 049.6\ km`

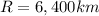
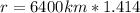
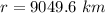
The distance (d) from the earth surface is calculated as thus;

`d = r - R`

`d = 9049.6\ km - 6400\ km`

`d = 2649.6\ km`

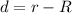
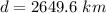
`d = 2650\ km` --- approximated