Answer:
Following are the solution to this question:
Step-by-step explanation:
In the following forms, RXS can appear:
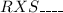 it may look like that really,
it may look like that really,
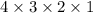 forms = 24 may construct the remainder of its letters.
forms = 24 may construct the remainder of its letters.
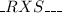 it may look like that really,
it may look like that really,
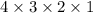 forms = 24 may construct the remainder of its letters.
forms = 24 may construct the remainder of its letters.
 it may look like that really,
it may look like that really,
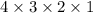 forms = 24 may construct the remainder of its letters.
forms = 24 may construct the remainder of its letters.
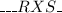 it may look like that really,
it may look like that really,
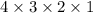 forms = 24 may construct the remainder of its letters.
forms = 24 may construct the remainder of its letters.
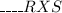 it may look like that really,
it may look like that really,
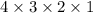 forms = 24 may construct the remainder of its letters.
forms = 24 may construct the remainder of its letters.
And we'll have a total of
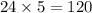 permutations with both the string RXS.
permutations with both the string RXS.
In the following forms, UZ can appear:
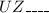 They can organize your remaining 5 characters through 5 categories! Procedures
They can organize your remaining 5 characters through 5 categories! Procedures

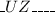 They can organize your remaining 5 characters through 5 categories! Procedures
They can organize your remaining 5 characters through 5 categories! Procedures

 They can organize your remaining 5 characters through 5 categories! Procedures
They can organize your remaining 5 characters through 5 categories! Procedures

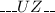 They can organize your remaining 5 characters through 5 categories! Procedures
They can organize your remaining 5 characters through 5 categories! Procedures

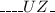 They can organize your remaining 5 characters through 5 categories! Procedures
They can organize your remaining 5 characters through 5 categories! Procedures

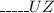 They can organize your remaining 5 characters through 5 categories! Procedures
They can organize your remaining 5 characters through 5 categories! Procedures

There may be
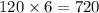 ways of complete permutations.
ways of complete permutations.