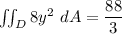Answer:
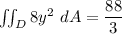
Explanation:
The equation of the line through the point
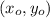 &
&
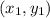 can be represented by:
can be represented by:
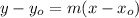
Making m the subject;
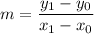
∴
we need to carry out the equation of the line through (0,1) and (1,2)
i.e
y - 1 = m(x - 0)
y - 1 = mx
where;
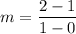
m = 1
Thus;
y - 1 = (1)x
y - 1 = x ---- (1)
The equation of the line through (1,2) & (4,1) is:
y -2 = m (x - 1)
where;
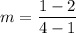
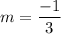
∴
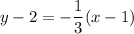
-3(y-2) = x - 1
-3y + 6 = x - 1
x = -3y + 7
Thus: for equation of two lines
x = y - 1
x = -3y + 7
i.e.
y - 1 = -3y + 7
y + 3y = 1 + 7
4y = 8
y = 2
Now, y ranges from 1 → 2 & x ranges from y - 1 to -3y + 7
∴
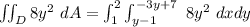
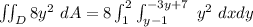
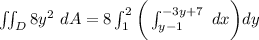
![\iint_D 8y^2 \ dA =8 \int^2_1 \bigg ( [xy^2]^(-3y+7)_(y-1) \bigg ) \ dy](https://img.qammunity.org/2021/formulas/mathematics/college/vkzo3n8qjb72cwkqk2oxispl2uos6vlxts.png)
![\iint_D 8y^2 \ dA =8 \int^2_1 \bigg ( [y^2(-3y+7-y+1)]\bigg ) \ dy](https://img.qammunity.org/2021/formulas/mathematics/college/5xgv5gb9ojrpx1od75taep9rbxvx9y0ys9.png)
![\iint_D 8y^2 \ dA =8 \int^2_1 \bigg ([y^2(-4y+8)] \bigg ) \ dy](https://img.qammunity.org/2021/formulas/mathematics/college/p7ut55iw79r8lug233g0jrbh5vgs4r9jg0.png)
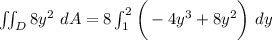
![\iint_D 8y^2 \ dA =8 \bigg [( -4y^4)/(4)+(8y^3)/(3) \bigg ]^2_1](https://img.qammunity.org/2021/formulas/mathematics/college/slkxn1gnk1d2kurhnntwa6ucrzguaei31s.png)
![\iint_D 8y^2 \ dA =8 \bigg [ -y^4+(8y^3)/(3) \bigg ]^2_1](https://img.qammunity.org/2021/formulas/mathematics/college/lka36n67zlyba9uj4jofgbopolumiy28o2.png)
![\iint_D 8y^2 \ dA =8 \bigg [ -2^4+(8(2)^3)/(3) + 1^4- (8* (1)^3)/(3)\bigg]](https://img.qammunity.org/2021/formulas/mathematics/college/5hw3mb9tk4qr5jc2giqo9qguuwsl1vs1ca.png)
![\iint_D 8y^2 \ dA =8 \bigg [ -16+(64)/(3) + 1- (8)/(3)\bigg]](https://img.qammunity.org/2021/formulas/mathematics/college/mtg6ht4s1ulvly6hv2npwd6pdalpgdd5hs.png)
![\iint_D 8y^2 \ dA =8 \bigg [ -15+ (64-8)/(3)\bigg]](https://img.qammunity.org/2021/formulas/mathematics/college/7s2kz6px3oc4l2e60m3rclxz6jobzarygn.png)
![\iint_D 8y^2 \ dA =8 \bigg [ -15+ (56)/(3)\bigg]](https://img.qammunity.org/2021/formulas/mathematics/college/7pj26utyjh2kyohywbx0w2h2uaboyaxn5p.png)
![\iint_D 8y^2 \ dA =8 \bigg [ (-45+56)/(3)\bigg]](https://img.qammunity.org/2021/formulas/mathematics/college/uhb2rnji12ecsgd47kdd3ut1rwtsd21rzn.png)
![\iint_D 8y^2 \ dA =8 \bigg [ (11)/(3)\bigg]](https://img.qammunity.org/2021/formulas/mathematics/college/xfeh8pb4txsedy9h6fxgxg560epfzvmvff.png)