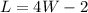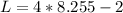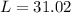Answer:

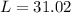
Explanation:
Let L = Length and W = Width.
So:
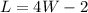
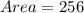
Required
Find L and W
Area is calculated as:
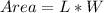
Substitute 4W - 2 for L and 256 for Area

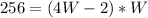
Open Bracket

Divide through by 2
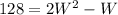
Equate to 0

An equation
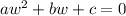 has the roots
has the roots
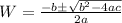
Where
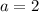
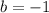

So:
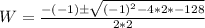
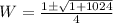


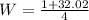 or
or
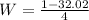
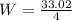 or
or
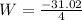
 or
or
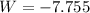
But the dimension can not be negative.
So:

Recall: