Question

Susie is solving the quadratic​

Answer 1

Option (D)

Explanation:

Standard equation of a quadratic function is,

ax² + bx + c

Comparing this function with the given quadratic function,

f(x) = 2x² - 4x - 3

a = 2, b = -4 and c = -3

By using quadratic formula to get the value of x,

x =
`(-b\pm √(b^2-4ac) )/(2a)`

=
`(-(-4)\pm √((-4)^2-4(2)(-3)) )/(2(2))`

=
`(4\pm√(16+24))/(4)`

=
`(-4\pm √(40))/(4)`

=
`(-2\pm √(10))/(2)`

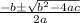
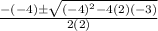
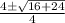
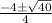
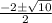
Therefore, Susie made a mistake in step IV.

Option (D) is the answer.