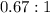Answer:
The ratio is
Step-by-step explanation:
From the question we are told that
The activation energy separating the equatorial and the axial form is

Generally according to the Boltzmann distribution , the relationship between concentration(in terms of number of molecule) of the equatorial form and the concentration of the axial form is mathematically represented as

Here
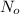 is the number of molecule in equatorial form and N is the number of the molecules in the axial form.
is the number of molecule in equatorial form and N is the number of the molecules in the axial form.
R is the gas constant with value
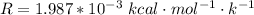
T is the temperature of the room with value
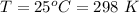
So

=>

So the ratio of the concentration of equatorial form to the axial form is