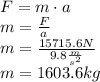Question

Los muelles de un remolque están calibrados para soportar su peso, cuando se carga el remolque con 2100 kg, la fuerza ejercida es de 20580 N comprime los muelles de un remolque 5,5 cm a)Longitud que desciende el remolque si se carga con 28000 N b)Si ha descendido 4,2 cm la carga

Answer 1

a) El remolque desciende 7.4 cm

b) La carga debe ser de 15715.6 N ó 1603.6 kg

Step-by-step explanation:

Para los cálculos que involucren muelles, se aplica la Ley de Hooke, la cual relaciona el efecto de una Fuerza y el cambio de longitud que esta ejerce, en un resorte de elasticidad dada.

Escrito en fórmula:

`F=-k \cdot \Delta L`

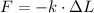
Donde:

F es la fuerza ejercida

k es la constante elástica del muelle

ΔL es la variación de longitud del muelle

El problema indica que al cargar 2100 kg se ejerce una fuerza de 20580 N

Esto se corrobora con la 2da ley de Newton y asumiendo una aceleración de gravedad de 9.8
`(m)/(s^(2) )`

`F_(1) =m \cdot a\\F_(1)=2100kg \cdot 9.8(m)/(s^2)\\F_(1)=20580N`

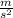
Esta fuerza comprime o reduce la longitud del muelle en 5.5 cm. Usando estos datos en la Ley de Hooke, podemos obtener la constante elástica k:

`F=-k \cdot \Delta L\\20580N=-k \cdot (-0.055m)\\\\k=(20580N)/(0.055m)\\k= 374181(N)/(m)`

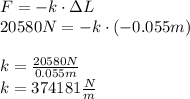
Ahora ya tenemos los datos para resolver las preguntas:

• a) Longitud que desciende el remolque si se carga con 28000 N

Aplicando directamente la formula de la Ley de Hooke:

`F=-k \cdot \Delta L\\\Delta L=(F)/(-k) \\\Delta L= (28000N)/(-374181(N)/(m)) \\\Delta L=-0.074 m = -7.4cm`

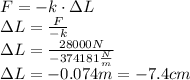
• b) Si ha descendido 4,2 cm la carga

En este caso debemos calcular la fuerza necesaria que haga descender el remolque 4.2cm. Nuevamente utilizando la Ley de Hooke con estos nuevos datos:

`F=-k \cdot \Delta L\\F=-374181(N)/(m) \cdot (-0.042m)\\F=15715.6N`

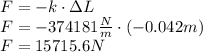
Si queremos saber la carga en kilogramos:

`F = m \cdot a\\m = (F)/(a) \\m = (15715.6N)/(9.8(m)/(s^2) )\\m= 1603.6 kg`