Question

A ball is thrown vertically upward from the top of a 96-ft tower, with an initial velocity of 16 ft/sec. Its position function is s(t) = -16t2 + 16t + 96. What is its velocity in ft/sec when it hits the ground?

Answer 1

80 ft/s

Explanation:

Given that,

A ball is thrown vertically upward from the top of a 96-ft tower, with an initial velocity of 16 ft/sec. Its position function is given by :

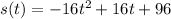`s(t)=-16t^2 + 16t + 96` ...(1)

When it hits the ground, s(t) = 0

`-16t^2 + 16t + 96=0\\\\t=3\ s`

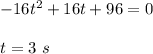
At t = 3 s it will hit the fround.

We need to find its velocity when it hits the ground.

Differentiate equation (1) to find its velocity.

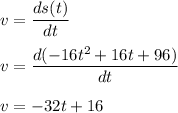`v=(ds(t))/(dt)\\\\v=(d(-16t^2 + 16t + 96))/(dt)\\\\v=-32t+16`...(2)

Put t = 3 in equation (2)

`v=-32(3)+16\\\\v=-80\ ft/s`

Hence, when it will ground its velocity is 80 ft/s.