Given:
Distance between to cities = 500 mi
Two cars left simultaneously moving towards each other.
The speed of one car was 10 mph greater than the speed of the other car.
They meet in 5 hours.
To find:
The speed of each car.
Solution:
Let x mi/h be the speed of one car.
So, speed of second car = (x + 10) mi/h
Two cars left simultaneously moving towards each other.
So, their relative speed = x + (x+10) = (2x+10) mi/h
We know that,

On substituting the values, we get
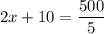
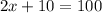
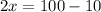

Divide both sides by 2.
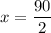
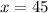
Now,
Speed of one car = 45 mi/h
Speed of other car = 45+10
= 55 mi/h
Therefore, the speeds of two cars are 45 mi/h and 55 mi/hr.