Question

Electromagnetic radiation is emitted by accelerating charges. The rate at which energy is emitted from an accelerating charge that has charge q and acceleration a is given by dEdt=q2a26πϵ0c3 where c is the speed of light.Part AIf a proton with a kinetic energy of 5.0 MeV is traveling in a particle accelerator in a circular orbit with a radius of 0.530 m , what fraction of its energy does it radiate per second?(dE/dt)⋅1sE =

Answer 1

P /K = 1,997 10⁻³⁶ s⁻¹

Step-by-step explanation:

For this exercise let's start by finding the radiation emitted from the accelerator

`(dE)/(dt)` =
`(q^(2) a^(2) )/(6\pi \epsilon_(o) c^(2) )`

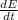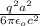
the radius of the orbit is the radius of the accelerator a = r = 0.530 m

let's calculate

\frac{dE}{dt} = [(1.6 10⁻¹⁹)² 0.530²] / [6π 8.85 10⁻¹² (3 108)³]

P= \frac{dE}{dt}= 1.597 10⁻⁵⁴ W

Now let's reduce the kinetic energy to SI units

K = 5.0 10⁶ eV (1.6 10⁻¹⁹ J / 1 eV) = 8.0 10⁻¹⁹ J

the fraction of energy emitted is

P / K = 1.597 10⁻⁵⁴ / 8.0 10⁻¹⁹

P /K = 1,997 10⁻³⁶ s⁻¹