Question

If the product of the two roots of the equation : (k - 2) x2 - 6 X + 12 = 0 is 3, then k =

(a) zero
(b) 4
(c) 6
(d) 38​

Answer 1

(c)

Explanation:

Given a quadratic equation in standard form

ax² + bx + c = 0

Then the product of the roots =
`(c)/(a)`

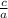
(k - 2)x² - 6x + 12 = 0 ← is in standard form

with a = k - 2 and c = 12 , thus

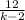`(12)/(k-2)` = 3 ( multiply both sides by (k - 1) )

12 = 3(k - 2) = 3k - 6 ( add 6 to both sides )

18 = 3k ( divide both sides by 3 )

6 = k → (c)