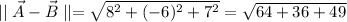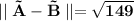Since vector B was not specified, I'll assume one at random. You can later answer your own question.
Answer:
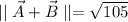
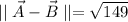
Step-by-step explanation:
Given:
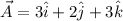
And (assumed):
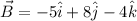
Find the magnitude of
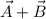

Given a vector
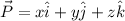
The magnitude of the vector is:
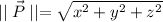
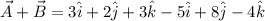
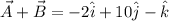
The magnitude of the sum is:
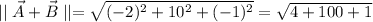
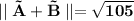
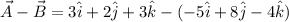
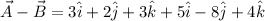
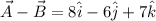
The magnitude of the difference is: