Question

A car of mass 1000 kg travelling at a velocity of 25 m/s collides with another car of mass 1500kg which is at rest. The two cars stick and move off together. What is the velocity of the two cars after the collision?​

Answer 1

Please find attached photograph for your answer.

Answer 2

The velocity of the two cars is 10 m/s after the collision.

Step-by-step explanation:

Law Of Conservation Of Linear Momentum

The total momentum of a system of bodies is conserved unless an external force is applied to it. The formula for the momentum of a body with mass m and velocity v is

P=m.v

If we have a system of bodies, then the total momentum is the sum of them all

`P=m_1v_1+m_2v_2+...+m_nv_n`

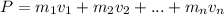
If some collision occurs, the velocities change to v' and the final momentum is:

`P'=m_1v'_1+m_2v'_2+...+m_nv'_n`

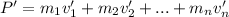
In a system of two masses, the law of conservation of linear momentum takes the form:

`m_1v_1+m_2v_2=m_1v'_1+m_2v'_2`

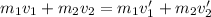
If both masses stick together after the collision at a common speed v', then:

`m_1v_1+m_2v_2=(m_1+m_2)v'`

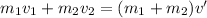
The car of mass m1=1000 Kg travels at v1=25 m/s and collides with another car of m2=1500 Kg which is at rest (v2=0).

Knowing both cars stick and move together after the collision, their velocity is found solving for v':

`\displaystyle v'=(m_1v_1+m_2v_2)/(m_1+m_2)`

`\displaystyle v'=(1000*25+1500*0)/(1000+1500)`

`\displaystyle v'=(25000)/(2500)`

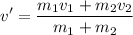
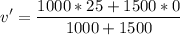
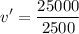
v' = 10 m/s

The velocity of the two cars is 10 m/s after the collision.