1 Answer

Stephen Curran · Answer 1 · 2021-05-28T22:58:33+0000

I assume you're referring to the product,

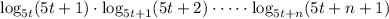
$\log_(5t)(5t+1)\cdot\log_(5t+1)(5t+2)\cdot\cdots\cdot\log_(5t+n)(5t+n+1)$

Recall the change-of-base identity:

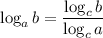
$\log_ab=(\log_cb)/(\log_ca)$

where c > 0 and c ≠ 1. This means the product is equivalent to

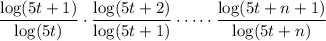
$(\log(5t+1))/(\log(5t))\cdot(\log(5t+2))/(\log(5t+1))\cdot\cdots\cdot(\log(5t+n+1))/(\log(5t+n))$

and it telescopes in the sense that the numerator and denominator of any two consecutive terms cancel with one another. The above then simplifies to

$(\log(5t+n+1))/(\log(5t))=\boxed{\log_(5t)(5t+n+1)}$

Please log in or register to add a comment.