Question

Birdman is flying horizontally at a

speed of 40 m/s and a height of 58
m. Birdman releases a turd directly
above the start of the field. How far
from the start of the field should the
robot hold the bucket to catch the
turd?

Answer 1

The robot should hold the bucket at 137.6 m from the start of the field

Step-by-step explanation:

Horizontal Motion

When an object is launched horizontally with a speed v from a height h, it describes a curved path exclusively ruled by gravity until it eventually hits the ground.

The range or maximum horizontal distance d traveled by the object can be calculated as follows:

`\displaystyle d=v\cdot\sqrt{\frac {2h}{g}}`

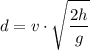
Birdman flies horizontally at a speed of v=40 m/s and a height of h=58 m. He releases a turd above the start of the field. If the robot was exactly down Birdman, then it won't catch the turd with the bucket because it would land farther away by a distance equal to the range. Thus:

`\displaystyle d=40\cdot\sqrt{\frac {2*58}{9.8}}`

`\displaystyle d=40\cdot√(11.84)`

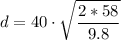
d = 137.6 m

The robot should hold the bucket at 137.6 m from the start of the field