I assume you know that there are n total n-th roots for any non-zero complex number.
(If you're looking for "the" principal root, you'll have to specify which branch you're calling the principal branch of the n-th root function.)
Start by writing
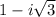 in exponential form. We have modulus/magnitude
in exponential form. We have modulus/magnitude
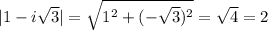
and
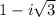 lies in the fourth quadrant of the complex plane, so its argument is
lies in the fourth quadrant of the complex plane, so its argument is

Then the exponential form is
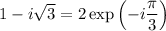
(where
 , if you're not familiar with the notation)
, if you're not familiar with the notation)
By de Moivre's theorem, we have the fourth roots
![\sqrt[4]{1 - i\sqrt3} = \sqrt[4]{2} \exp\left(i \frac{-\frac\pi3+2k\pi}4\right)](https://img.qammunity.org/2023/formulas/mathematics/high-school/gkjhagjfplmp0y5jwdemvkqg9rl4z8l9bc.png)
where
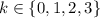 , so that we have a choice of
, so that we have a choice of
![\sqrt[4]{1 - i\sqrt3} = \begin{cases} \sqrt[4]{2} \exp\left(-i\frac\pi{12}\right) \\\\ \sqrt[4]{2} \exp\left(i(5\pi)/(12)\right) \\\\ \sqrt[4]{2} \exp\left(i(11\pi)/(12)\right) \\\\ \sqrt[4]{2} \exp\left(i(17\pi)/(12)\right) = \sqrt[4]{2} \exp\left(-i(7\pi)/(12)\right) \end{cases}](https://img.qammunity.org/2023/formulas/mathematics/high-school/nnrffisovuhutyronrvtcw782dh1pzv5fw.png)
(I rewrote the exponent to the last root just to be consistent about having each argument between -π and π radians)
If you want these in rectangular form (a + bi), sorry, that's where I draw the line; it can be done with simple trigonometry and algebra, but it's rather tedious, and the exponential forms are far more compact.