Question

For what value of k will the lines x+2y=0, 3x-4y-10=0 and 5x+ky-7=0 are concurrent?​

Answer 1

After solve the equations we get value of k=3

Explanation:

We need to find value of k for which the lines x+2y=0, 3x-4y-10=0 and 5x+ky-7=0 are concurrent.

If the lines are concurrent, they pass through same point.

Let:

`x+2y=0--eq(1)\\ 3x-4y-10=0--eq(2)\\ 5x+ky-7=0--eq(3)`

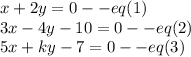
First solving equation 1 and 2 to find values of x and y

From eq(1) we find value of x and put it in eq(2)

`From \ eq(1) x+2y=0\\x=-2y\\Put x=-2y \ in \ eq(2)\\3x-4y-10=0\\3(-2y)-4y-10=0 \\-6y-4y=10\\-10y=10\\y=(10)/(-10)\\y=-1`

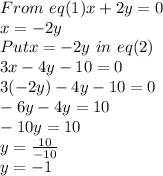
After solving we get value of y=-1

Now putting in eq(1) to get value of x

`x+2y=0\\x+2(-1)=0\\x-2=0\\x=2`

So, Value of x= 2

Now put value of x=2 and y=-1 into eq(3) to find value of k

`5x+ky-7=0\\5(2)+k(-1)-7=0\\10-k-7=0\\-k+3=0\\-k=-3\\k=3`

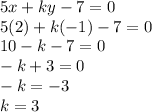
So, After solve the equations we get value of k=3