Answer:
The measure of the angle between the vectors = Ф = 11.30°
Explanation:
Given
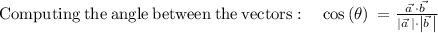
Next, find the lengths of the vectors:
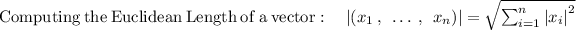
u = ⟨2, –3⟩
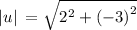
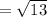
u = ⟨2, –3⟩
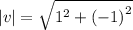
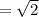
Finally, the angle is given by:
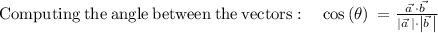
cos (Ф) = 5/√26
Ф = arc cos (cos (Ф)) = arc cos (5 √26) / (26)
Ф = 11.30°
Thus, the measure of the angle between the vectors = Ф = 11.30°