Given:
Endpoints of a line segment AB are A(2,3) and B(8,11).
To find:
(1) Slope of AB.
(2) Length of AB.
(3) Midpoint of AB.
(4) Slope of a line perpendicular to AB.
Solution:
We have, endpoints of line segment AB, A(2,3) and B(8,11).
(1)
Slope of AB is
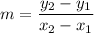
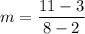
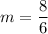
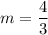
Therefore, the slope of AB is
 .
.
(2)
Length of AB is
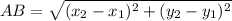
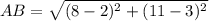
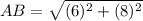
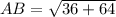
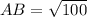
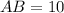
Therefore, the length of AB is 10 units.
(3) Midpoint of AB is
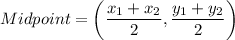
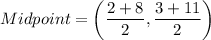
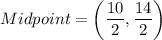
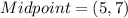
Therefore, the midpoint of AB is (5,7).
(4)
Product of slopes of two perpendicular lines is -1.
Let the slope of line perpendicular to AB be m₁.
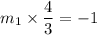
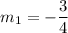
So, slope of line perpendicular to AB is
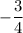 .
.