Question

Assuming normality, construct the requested confidence interval.

A sociologist is interested in the age at which a mother has her first child. A random sample of 20 recent births yielded an average maternal age to be 30 years with a standard deviation of 6.2 years.

Construct a 99% confidence interval for the mean age at which a mother has her first child.

Can I have some help with solving this problem with a TI84 calculator?

Answer 1

The appropriate response is "(26.03, 33.97)".

Explanation:

The given values are:

Average maternal age,

`\bar{x} = 30`

Standard deviation,

s = 6.2

Random sample,

n = 20

Now,

The degree of freedom will be:

⇒
`df=n-1`

`=20-1`

`=19`

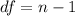
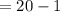
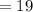
"t" at confidence level 99%, will be:

⇒
`\alpha=1-99 \ percent`

`=1-0.99`

`=0.01`

⇒
`(\alpha)/(2)=(0.01)/(2)`

`=0.005`

⇒
`t(\alpha)/(2) \ df=t \ 0.005,19`

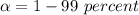
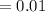
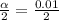
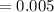
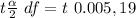
By using the student table, we get

`=2.86 1`

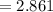
The margin of error will be:

⇒
`E=(t \alpha)/(2,df* ((s)/(√(n))))`

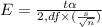
On substituting the estimated values, we get

⇒
`=2.861* ((6.2)/(√(20)))`

⇒
`=3.97`

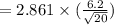
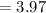
At 99%, the confidence level will be:

⇒
`\bar{x}-E< \mu <\bar{x}+E`

⇒
`30-3.97< \mu < 30+3.97`

⇒
`(26.03,33.97)`

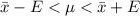
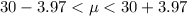
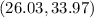
Thus the above is the correct approach.