Question

Which ordered pair is a solution to the following system of inequalities?

y < –x2 + x

y > x2 – 4

(0, –1)
(1, 1)
(2, –3)
(3, –6)

Answer 1

Answer: (0,-1)

Explanation:

Let's start with the first inequality,
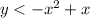`y < -x^(2)+x`. To check which points satisfy this inequality, we can substitute the x- and y-coordinates and see if they satisfy the inequality.

• A)
  `-1 < -0^(2)+0 \longrightarrow -1 < 0 \longrightarrow \text{ True}`
• B)
  `1 < -1^(2)+1 \longrightarrow 1 < 0 \longrightarrow \text{ False}`
• C)
  `-3 < -2^(2)+2 \longrightarrow -3 < -2 \longrightarrow \text{ True}`
• D)
  `-6 < -3^(2)+3 \longrightarrow -6 < -6 \longrightarrow \text{ False}`

Once again, we can repeat this for the second inequality (but this time, we only need to check the points that satisfy the first inequality).

• A)
  `-1 > 0^(2)-4 \longrightarrow -1 > -4 \longrightarrow \text{ True}`
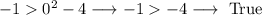
• C)
  `-3 > 2^(2)-4 \longrightarrow -3 > 0 \longrightarrow \text{ False}`

Therefore, the answer is (A) (0, -1).