Answer:
D) The vertex of the equation is
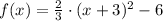 . The standard form of the equation is
. The standard form of the equation is
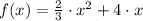 .
.
Explanation:
Let
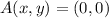 and
and
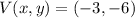 (vertex).
(vertex).
If we know that
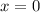 ,
,
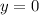 ,
,
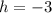 and
and
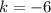 , then the standard equation results in:
, then the standard equation results in:
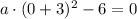
And the value of
 is:
is:
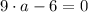
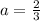
And the vertex form of the equation is
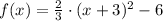 .
.
Lastly, the standard form of the equation is found by algebraic means:
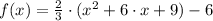
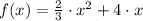
The standard form of the equation is
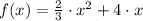 .
.
In consequence, the right answer is D.