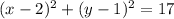Answer:
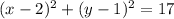
Explanation:
The current equation of the circle is:
⇒
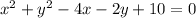
In order to get it into the standard form;
⇒
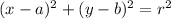
We must complete the square;
⇒
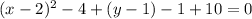
Now, collect like terms and rearrange;
⇒
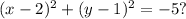
We now know that the Centre is at the point (2, 1).
We can use the distance formula to find the radius;
⇒

⇒
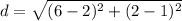
⇒
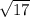
Therefore the radius squared is 17.
Now substitute into our equation:
⇒