Answer: D. 0.34
Step-by-step explanation:
Hardy-Weinberg Principle
The Hardy-Weinberg Principle is a theory in biology that represents populations of organisms that don't experience any changes in genotypic frequency from generation to generation. These populations must meet the following conditions:
- No genetic mutations
- Completely random mating
- No gene flow
- No selection (natural or artificial)
- An infinite population size
If a population meets these criteria, its genetic and allelic frequencies will remain constant and the population will be in Hardy-Weinberg Equilibrium. However, it is not possible for this to occur in nature, because at least one condition will always be violated in natural populations.
Hardy-Weinberg Equations
There are two important equations to use when doing problems like this. The first is p + q = 1. It represents the allelic frequency of the population.
- p = the frequency of the dominant allele
- q = the frequency of the recessive allele
The second equation is p² + 2pq + q² = 1, which shows the predicted frequencies of the three possible genotypes.
- p² = the genotype frequency of homozygous dominants
- 2pq = the genotype frequency of heterozygotes
- q² = the genotype frequency of homozygous recessives
Our Fly Problem
44 of our 100 organisms are green, and we know that to be green, they must have a homozygous recessive genotype (gg). That means that the frequency of homozygous recessives (q²) = 44/100 or 0.44. Since we have q², we can just take the square root to find q.
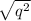 =
=
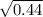
q = 0.66
Now, we can plug q into our first equation, p + q = 1.
p + 0.663 = 1
p = 0.337, or about 0.34
To make sure these are right, we can plug them into the Hardy-Weinberg equation to check!
p² + 2pq + q² = 1
(0.34)² + 2(0.34)(0.66) + (0.66)² = 1
0.1156 + 0.4488 + 0.4356 = 1
1 = 1