Answer
688.32m and 277.44m
Step-by-step explanation :
⠀

The X and Y coordinates of the rocket relative of firing
⠀
⠀
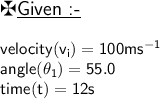
⠀
⠀
⠀
⠀
The horizontal range of projectile at x.
⠀
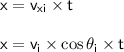
⠀
⠀

⠀
⠀

⠀
⠀
The vertical position of projectile at y.
⠀
⠀
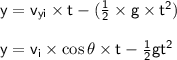
⠀
⠀

⠀
⠀

⠀
⠀
⠀
Henceforth, the distance at horizon is 688.32m and at vertical is 277.44m.