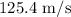Question

Doug hits a baseball straight towards a 15 ft high fence that is 400 ft from home plate. The ball is hit 2.5ft above the ground and leaves the bat at an angle of 30∘ with the horizontal. Find the minimum initial velocity needed for the ball to clear the fence.

Answer 1

`125.4\ \text{m/s}`

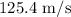
Explanation:

u = Initial velocity of baseball

`\theta` = Angle of hit =
`30^(\circ)`

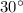
x = Displacement in x direction = 400 ft

y = Displacement in y direction = 15 ft

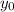`y_0` = Height of hit = 2.5 ft

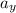`a_y` = g = Acceleration due to gravity =
`32.2\ \text{ft/s}^2`

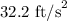
t = Time taken

Displacement in x direction

`x=u_xt\\\Rightarrow x=u\cos\theta t\\\Rightarrow t=(x)/(u\cos\theta)\\\Rightarrow t=(400)/(u\cos30^(\circ))\\\Rightarrow t=(400)/(u(√(3))/(2))\\\Rightarrow t=(800)/(u√(3))`

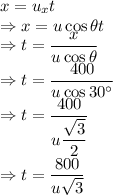
Displacement in y direction

`y=y_0+u_yt+(1)/(2)a_yt^2\\\Rightarrow y=y_0+u\sin\theta t+(1)/(2)a_yt^2\\\Rightarrow 15=2.5+u\sin30^(\circ)((800)/(u√(3)))+(1)/(2)* -32.2* ((800)/(u√(3)))^2\\\Rightarrow (400)/(√(3))-(10304000)/(3u^2)-12.5=0\\\Rightarrow 218.44=(10304000)/(3u^2)\\\Rightarrow u=\sqrt{(10304000)/(3*218.44)}\\\Rightarrow u=125.4\ \text{m/s}`

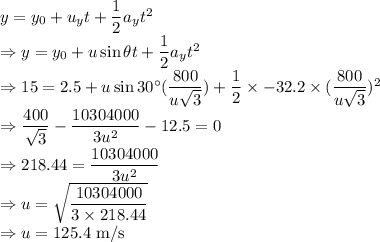
The minimum initial velocity needed for the ball to clear the fence is
`125.4\ \text{m/s}`