Answer:
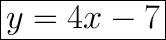
Explanation:
Linear equations will always be in the form
 , where m is the slope and b is the y-intercept
, where m is the slope and b is the y-intercept
Since we know nothing about this equation, other than the fact that there are two points in it, we must find the slope and the y-intercept.
Luckily, we have two points to work with. We know that the slope between two points will be the change in y divided by the change in x (
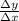 ), so we can use the two points given to us to find both changes.
), so we can use the two points given to us to find both changes.
The y value goes from 1 to 17, which is a
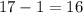 change.
change.
The x value goes from 2 to 6, which is a
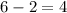 change.
change.
Now that we know both changes, we can divide the change in y by the change in x.

Now that we know the slope (4), we can plug it into our equation (
 ).
).
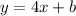
Now all we need to do is find the y-intercept. Since we know the slope and one of the points the line passes through, we can find the y-intercept by substituting in the values of x and y. Let's use the point (2, 1).
Therefore our y-intercept is -7. Now that we know the slope and the y-intercept, we can plug it into our equation.
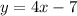
Hope this helped!