Hi there!
To solve, we need to find the distance traveled by the proton at which the proton's velocity reaches 0 m/s. This indicates the point at which the repulsive force caused by the line of charge and its consequential acceleration causes the proton to stop for an instant and be repelled back in the opposite direction.
For this, we can use the work-energy theorem to solve.
Recall the following equations:

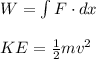
We will integrate along the path from the point 19.0 cm (0.19 m) from the line up to a point 'z' at which the proton has no kinetic energy (v = 0 m/s). This means that the wire will be doing NEGATIVE work on the proton as it is decreasing the proton's kinetic energy.
The equation for a force acting on a charged particle is given as:
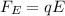
For an infinite line of charge, the electric field is given as:
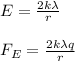
**λ = Linear charge density (C/m)
To set up our integral:

Integrate using the following natural log rule:
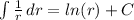
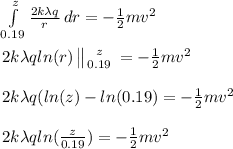
Now, we can begin solving for 'a'.
Move coefficients to one side:
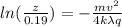
Take the base 'e' of both sides:

It will reach a distance 18.03 cm from the wire before it temporarily loses all of its kinetic energy (at rest) and begins to speed up in the opposite direction.