1 Answer

Peter Jamieson · Answer 1 · 2021-03-16T02:43:42+0000

Given:

Line segment NY has endpoints N(-11, 5) and Y(3,-3).

To find:

The equation of the perpendicular bisector of NY.

Solution:

Midpoint point of NY is

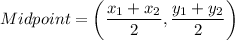
$Midpoint=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)$

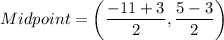
$Midpoint=\left((-11+3)/(2),(5-3)/(2)\right)$

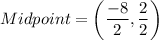
$Midpoint=\left((-8)/(2),(2)/(2)\right)$

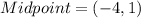
$Midpoint=\left(-4,1\right)$

Slope of lines NY is

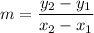
m=(y_2-y_1)/(x_2-x_1)

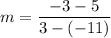
m=(-3-5)/(3-(-11))

m=(-8)/(14)

m=(-4)/(7)

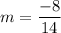
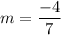
Product of slopes of two perpendicular lines is -1. So,

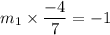
m_1* (-4)/(7)=-1

m_1=(7)/(4)

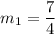
The perpendicular bisector of NY passes through (-4,1) with slope
(7)/(4) . So, the equation of perpendicular bisector of NY is

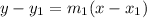
y-y_1=m_1(x-x_1)

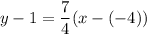
y-1=(7)/(4)(x-(-4))

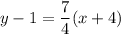
y-1=(7)/(4)(x+4)

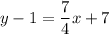
y-1=(7)/(4)x+7

Add 1 on both sides.

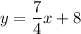
y=(7)/(4)x+8

Therefore, the equation of perpendicular bisector of NY is
.

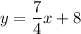Please log in or register to add a comment.