Answer:
The quotient when
 is divided by
is divided by
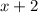 is
is
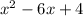 with no remainder, so x+2 is a factor of p(x).
with no remainder, so x+2 is a factor of p(x).
Explanation:
As the question suggests, there are two ways to solve this problem: long division (which can always be used to divide polynomials), and synthetic division (which can only be used when you are dividing by something of the form
 . In this case, we may use synthetic division, since
. In this case, we may use synthetic division, since
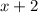 is equal to
is equal to
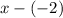 . I will use synthetic division here as it is slightly faster than long division.
. I will use synthetic division here as it is slightly faster than long division.
The -2 on the left represents that we are dividing by x-(-2), and the rest of the numbers in the top row are the coefficients of p(x): 1, -4, -8, and 8.
The first step in synthetic division is to being down the leading coefficient of the polynomial: in this case, the 1 (as indicated in red). Now, we multiply the 1 by -2. We get -2, which we place directly below the -4.
Next, we add directly down the column, (-4 + (-2) is equal to -6), and this answer is placed in the box below. We can continue this process, getting the coefficients 1, -6, 4, and 0 in the bottom row.
This is the answer: the quotient is
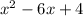 , and the remainder is zero (which indicates that x+2 is a factor of p(x)).
, and the remainder is zero (which indicates that x+2 is a factor of p(x)).
--
Edit: long division
We may also solve this problem using long division (see the second image). The first step is to look at the leading coefficients: since
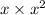 is equal to
is equal to
 , the first term in the quotient will be
, the first term in the quotient will be
 . Since
. Since
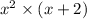 is equal to
is equal to
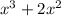 , we must now subtract that from
, we must now subtract that from
 .
.
We repeat the same process, as shown in the image. Since we eventually get to zero, the remainder is zero, and the polynomial at the top (x^2-6x+4) is the quotient.
I know this might be difficult to follow, so please comment if you have any questions.